Spearman's correlation Coefficient

range: [-1, 1]

summary

link: https://www.kaggle.com/code/dschettler8845/novo-esp-eda-baseline

• the formula:

  • $\rho =1-\frac{6\sum d_i^2}{n(n^2-1)}$

  • $r_s$ (or $\rho$) is the Spearman’s Correlation Coefficient

  • n is the number of points in the dataset

  • $d_i^2$ is the difference (in integer rank) between yhat and y

• the formula for non-integers:
  • $r_s={\rho }_{r{g}_X,r{g}_Y}=\frac{\text{cov}(r{g}_X,r{g}_Y)}{{\sigma }_{r{g}_X}{\sigma }_{r{g}_Y}}$
  • I assume that rg is the rank array of X and Y
  • https://www.kaggle.com/code/carlolepelaars/understanding-the-metric-spearman-s-rho/notebook
    • btw this notebook has good code for it using diff libraries
• The metric assesses how well the relationship between two variables can be described using a monotonic function
  • makes sense, cause it’s a correlation function
• Similar to Pearson’s Correlation Coefficient, however Spearman’s assesses monotonic relationships (whether linear or not)
• How to get a perfect score of +-1?
  • there are no duplicates

pros

• use when you want to make a model that can properly order n objects
  • you want the order of y_predicted to be in the same order as y_target

Cons

• https://statisticsbyjim.com/basics/spearmans-correlation/
  • doesn’t work for curvilinear relationships:
  • 
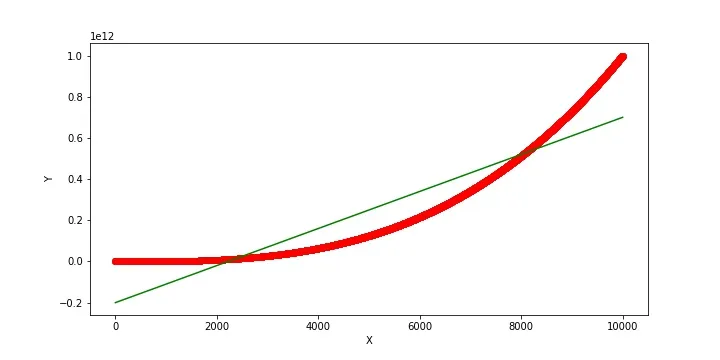
  • the red line is y, the green is yhat.
  • yhat doesn’t fit the data well, but the score is 0.92 (high!)
• Doesn’t work when your label column is unstable AND your target column can have duplicate labels
  • e.g. in Google QUEST Q&A Labeling, the question_type_spelling only had a few rare events
    • so ppl had to “fiddling with threshold values” (to determine which target label it should be postprocessed into)
    • this metric doesn’t work well for columns like this!
      • maybe MSE would’ve worked better, since a change in rank is a discrete jump in error

Important Considerations

• https://www.kaggle.com/c/google-quest-challenge/discussion/118724

  • The spearman’s correlation coefficient only considers the order of values

  • Even though array b is monotonically increasing, it has a lower spearman score

    a = np.array([0.5, 0.5, 0.7, 0.7]) b = np.array([4., 5., 6., 7.]) print_spearman(a, b) # ⇒ 0.89

    b2 = np.array([4., 4., 6., 6.]) print_spearman(a, b2) # ⇒ 1. ```

  • So it is important to predict whether consecutive terms are the same value

• why might this happen?
  • the target column in your dataset was evaluated using a rubric, not relative to the other rows