triplet mining

https://omoindrot.github.io/triplet-loss

• The goal of the triplet loss is to make sure that:
  • 1. Two examples with the same label have their embeddings close together in the embedding space
  • 2. Two examples with different labels have their embeddings far away.
• To formalise this requirement, the loss will be defined over triplets of embeddings:
  • an anchor
  • a positive of the same class as the anchor
  • a negative of a different class
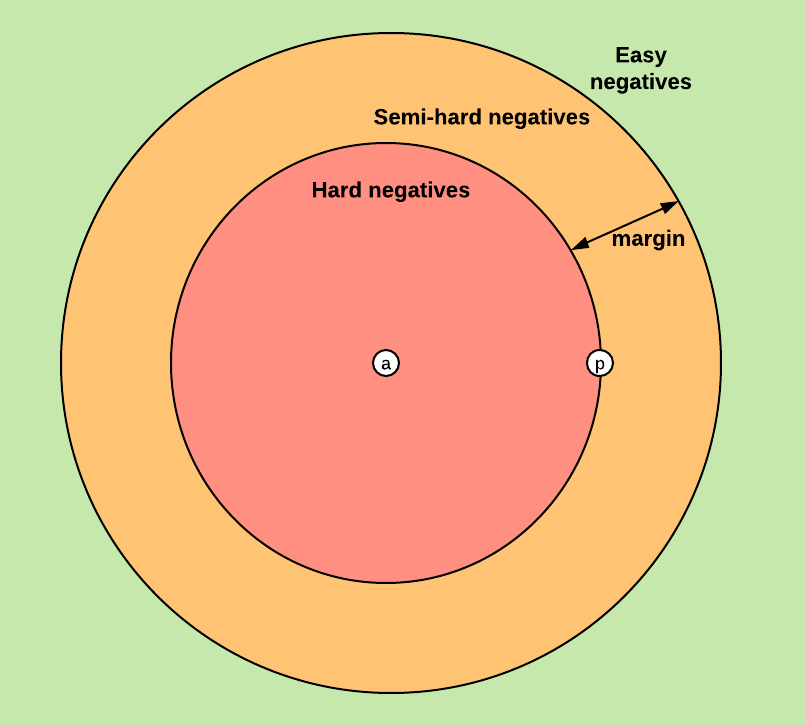
• For some distance on the embedding space d, the loss of a triplet (a,p,n) is:
  • $L=\max (d(a,p)-d(a,n)+\text{margin},0)$
  • where margin is a value we choose that says: “the negative should be farther away than the positive by this margin”
  • This loss pushes:
    • d(anchor, pos) to 0
    • d(anchor, neg) to be greater than d(anchor, pos) + margin
• hard negatives are examples that are closer to the anchor example than the positive example:
  • 
• online mining: we have computed a batch of B embeddings from a batch of B inputs. Now we want to generate triplets from these B embeddings.
  • batch all: select all the valid triplets, and average the loss on the hard and semi-hard triplets.
    • a crucial point here is to not take into account the easy triplets (those with loss 00), as averaging on them would make the overall loss very small
  • batch hard: for each anchor, select the hardest positive (biggest distance d(a,p)) and the hardest negative among the batch
    • works the best according to https://arxiv.org/abs/1703.07737
    • implementation:
      • to get the hardest positive:
        • 1. generate the pairwise distance matrix between all examples in the batch
        • 2. take the maximum distance over each row
      • to get the hardest negative (tricky, since we need to get the minimum distance for each row, and the diagonal is 0)
        • solution, just add infinity to the diagonal before getting the smallest value in the matrix
      • now calculate: triplet_loss = max(hardest_positive_dist - hardest_negative_dist + margin, 0.0)