- So the Fiedler vector ends up painting the graph in a gradient that goes from positive to negative. Each individual value 𝑥𝑖�� doesn’t mean much by itself. But the relative values do: clusters of vertices that are close together get similar values, and far-apart vertices often get different values.
- For the next eigenvector, we will add an additional constraint to our problem: we’ll be looking for a vector 𝐲� perpendicular to the Fiedler vector. Essentially, this says that 𝐲� should have similar properties, but be different from the thing we found just now, describing a different feature of the graph.
- For example, if our graph has three big and sparsely connected clusters, the Fiedler vector might assign positive values to one cluster and negative values to the other two. The next eigenvector might choose a different cluster to separate from the other two clusters. This distinguishes all the clusters, so the eigenvector after that will have to find some inter-cluster separation…
https://www.youtube.com/watch?v=FRZvgNvALJ4
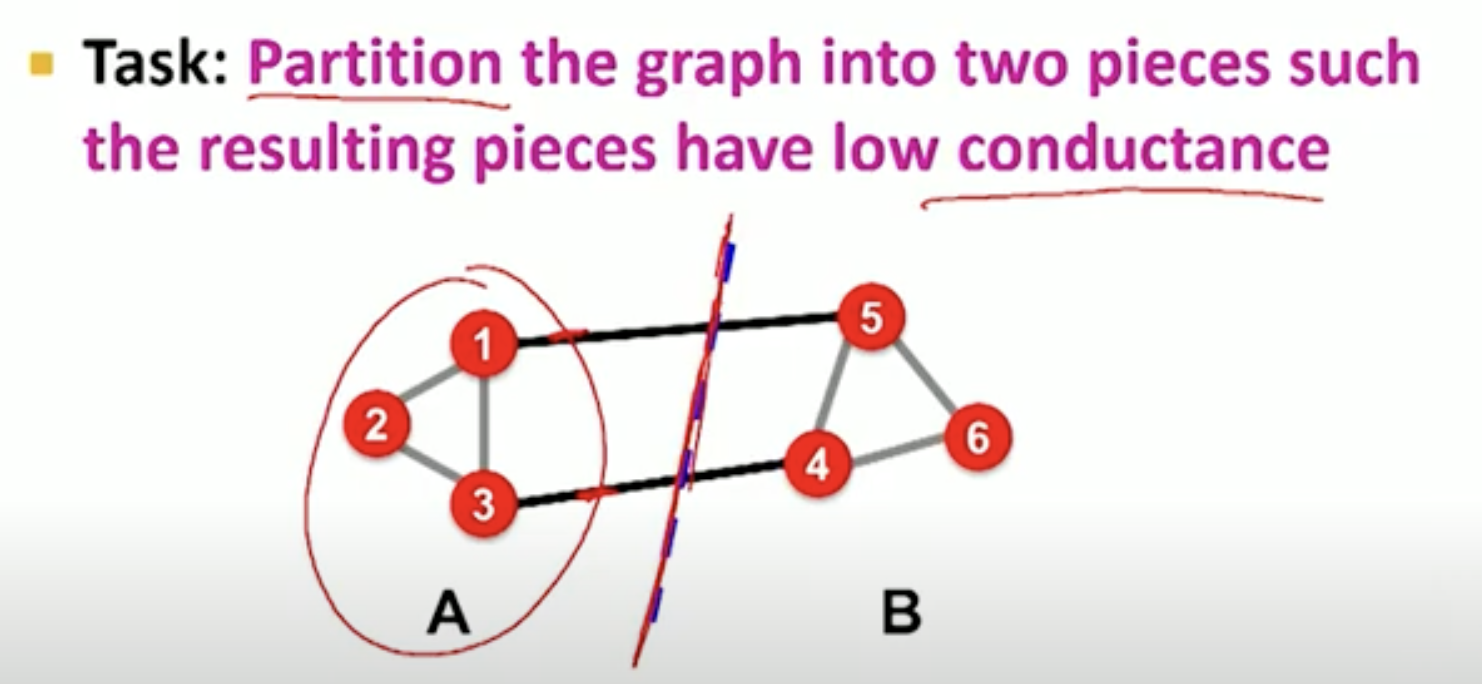
- What problem are we trying to solve:
- we are trying to split the graph into 2 pieces (identify clusters)
- defn clusters: a group of nodes in the graph that have many connections between each other, and few connections to external clusters
- defn conductance: the number of edges that connect between different clusters

- it makes sense for it to be the sum of neighbours. cause non-neighbours are 0 in the adj matrix!

- The point of Spectral Graph Theory: what do the eigen values and eigen vectors (of the adj matrix) tell us about the graph
- Examples of Eigendecompositions of Graphs