Evidence lower bound (ELBO) (aka variational Lower Bound)

(138) Evidence Lower Bound (ELBO) - CLEARLY EXPLAINED! - YouTube

• We want to make our model’s predictions $q_{\varphi }(z|x)$ match the ground truth $p_{\theta }(z|x)$

• This means we want to minimize KL divergence between the our model’s version of the distribution with the real distribution:

  • 
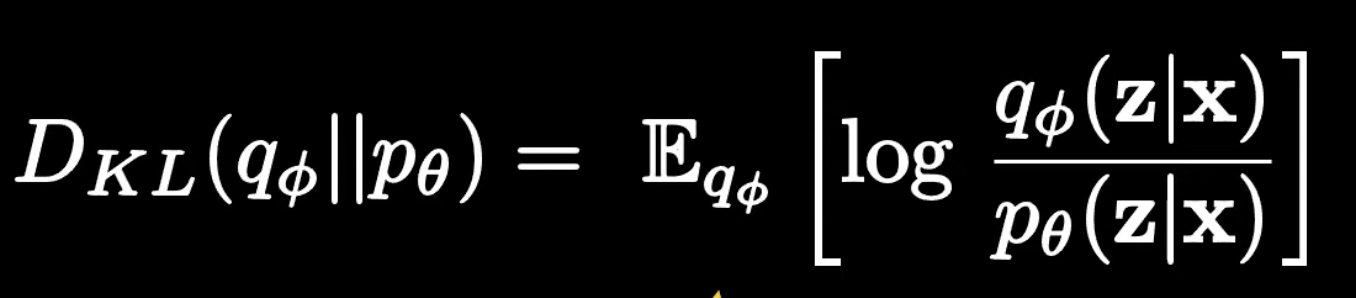
  • To use this kl divergence as the loss to our model, we need to perform the calculation
  • However, notice how the RHS includes the $p_{\theta (z|x)}$ term.
    • This is the real distribution of the data and we don’t know this!
    • if we did, we wouldn’t need to train the model!

• So let’s manipulate the KL divergence formula into a different form to see if we can minimize / maximize another objective within it to minimize the KL divergence.

• after manipulating, we get this:

• 

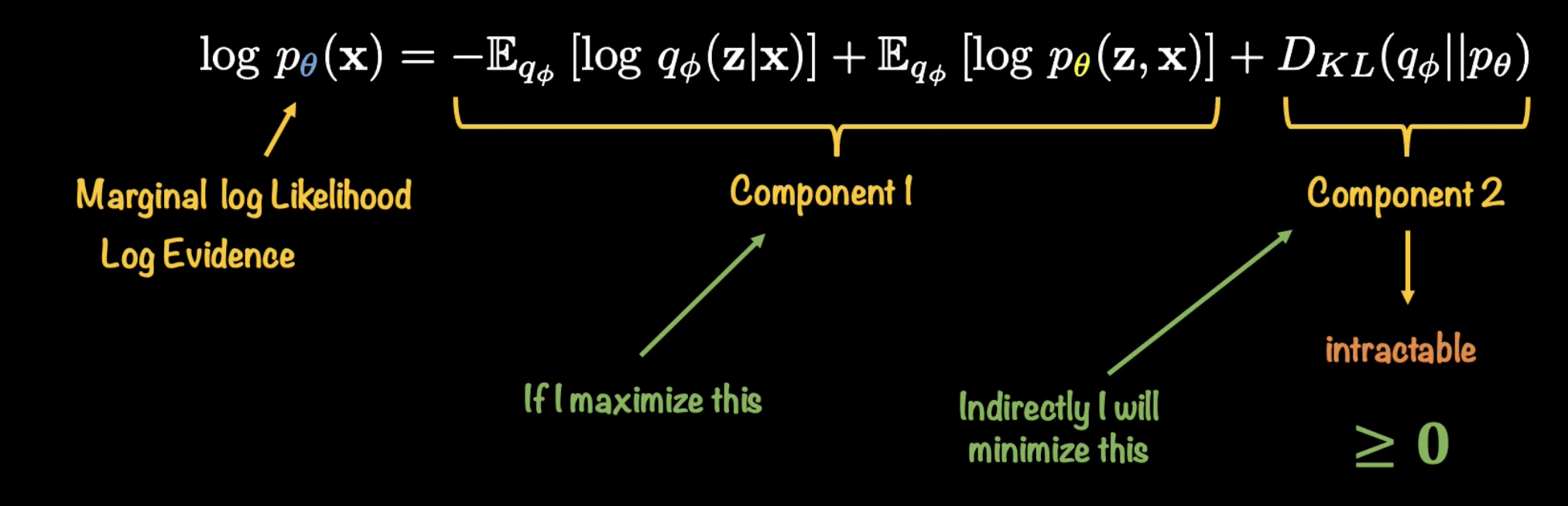
  • The Marginal log likelihood is the likelihood of the REAL distribution fitting the real data
    • this term is fixed
  • component 2 is the KL divergence from before. We can’t compute it
  • Notice if we maximize component 1, then we minimize the intractable KL divergence term (since the LHS is fixed)

• ELBO is component 1: $-E_{q_{\varphi }}[{\log }_{q_{\varphi }}(z|x)]+E_{q_{\varphi }}[{\log }_{p_{\theta }}(z,x)]$

• If we maximize, the ELBO, we indirectly minimize the KL divergence between our model and the real distribution

  • so our model gets more accurate!

• HOWEVER, this form of ELBO is too complicated. So let’s simplify it:

  • 
    • it’s called the reconstruction error since we’re reconstructing x from z
  • by minimizing this, we can make our model more accurate

• THE MOST IMPORTANT POINT

  • The KL divergence in the ELBO formula is different from the KL divergence from the start
    • this KL divergence is between our model and the REAL distribution of Z
      • the first KL divergence (the intractable one) is the divergence between our model and the conditional distribution of Z
    • in blogs, ppl will mention KL divergence, but since this KL divergence term looks very similar to the original one, it’s easy to get confused
      • people will also NOT point out that it’s not the same

Scratchpad 2

$D_{KL}(q_{\varphi }||p_{\theta })=E_{q_{\varphi }}[\log \frac{q_{\theta }(z|x)}{p_{\theta }(z|x)}]$

• https://blog.evjang.com/2016/08/variational-bayes.html

  • Assume we have a hidden variable that dictates the observed variable

  • 

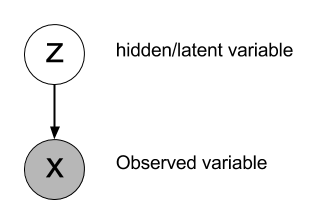
  • e.g.

    • X is the “raw pixel values of an image”
    • Z = 1 means: “the img is a cat”

  • We care about P(Z|X) (the posterior inference):

    • Given this surveillance footage X, did the suspect show up in it?
    • Given historical stock prices $X_{1:t}$, what will $X_{t+1}$ be?

  • Since P(Z|X) is too hard to know exactly, we train models $Q_{\theta }(Z|X)$ that matches P(Z|X) as close as possible

    • We could try to use sampling-based approaches like MCMC, but these are slow to converge..

  • The log-likelihood of the observed data can be decomposed into two terms: log P(X) = L(Q) + KL(Q || P)

    • P(X) is the probability distribution of X
      • e.g. There are 10 dogs and 15 cats in the dataset
    • L(Q) is the variational lower bound
    • KL(Q || P) is the KLDivergenceLoss
    • derivation: https://xyang35.github.io/2017/04/14/variational-lower-bound/

  • The KL divergence is always non-negative, which means that L(Q) is always less than or equal to the true log-likelihood log P(X). Hence, L(Q) serves as a lower bound on the log-likelihood.

  • The goal of variational inference is to maximize the variational lower bound L(Q) with respect to the parameters of the variational distribution Q(Z). By maximizing the lower bound, we indirectly minimize the KL divergence between Q(Z) and P(Z|X)

    • so our model’s distribution Q(Z) is brought closer to P(Z|X) (and thus makes better predictions)

  • The term “variational” in “variational lower bound” comes from the fact that the approximation is based on variational calculus, which involves optimizing over a family of functions (in this case, the variational distributions).

• since log P(X) = L(Q) + KL(Q || P)
  • rearranging, we get: L(Q) = log P(X) - KL(Q || P)
  • since maximizing L(q) makes the model better, we can also minimize -L(q) to make the model better
  • Therefore, loss functions look like this: Loss_vb = KL(Q || P) - log P(X)

Scratchpad

• It’s the lower bound on the log-likelihood of some observed data
• https://xyang35.github.io/2017/04/14/variational-lower-bound/ - The definition is: $L=E_q[\log p(X,Z)]+H[Z]$
• Where
  • Z is the hidden / latent variable
  • X is the observed variable
    • There is an unknown relationship about how the distribution of Z affects the distribution of X
  • H is entropy
• The derivation
  • 
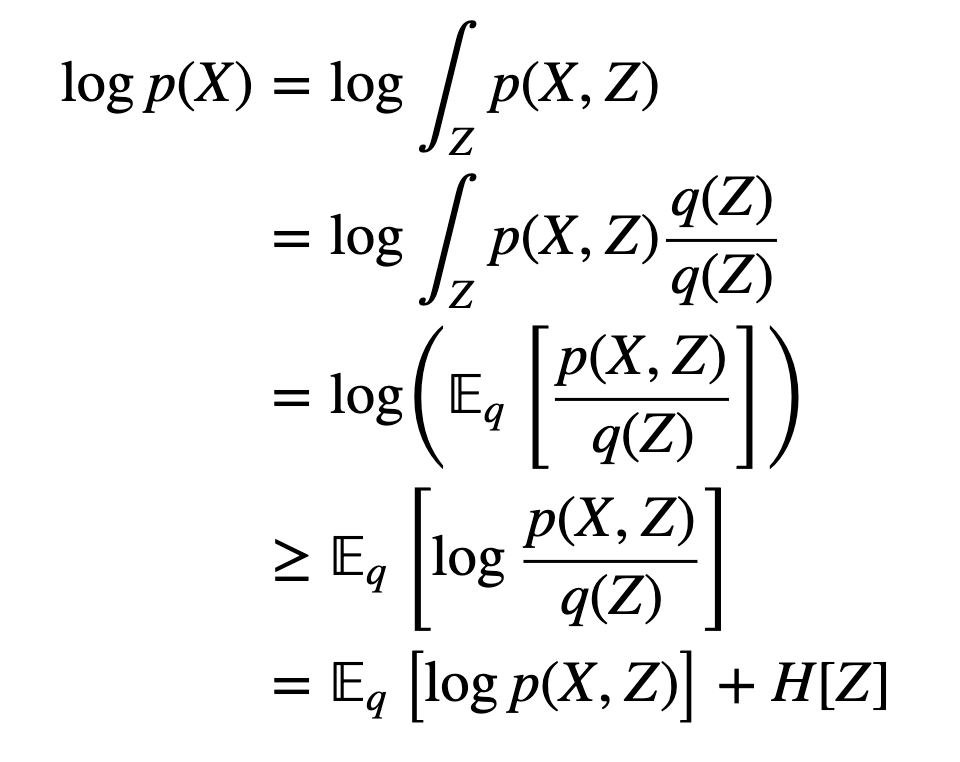
    • the first line comes from the law of total probability
    • The last line is L (variational Lower Bound)
• Why do we care about L?
  • cause if we want our model’s outputs (Z) to match the distribution of the training data(X), we want P(Z | X) to be very close to 1
• Since we are dealing with logs multiplied by probabilities, it looks like KLDivergenceLoss
  • so another way to express L is:
    • $L=\log p(X)-KL[q(Z)||p(Z|X)]$
• Evidence Lower Bound (ELBO) - CLEARLY EXPLAINED! (youtube.com)